工程能力と工程性能

製造業の品質保証体系としてISO,IATFと呼ばれるものがある。
欧米の自動車メーカーなどは特にサプライヤーに対してこの認証取得を求めている。
この体系のコアツールの一つとして工程能力(Cp,Cpk)と工程性能(Pp,Ppk)がある。
単純にいえば、ある製品もしくは工程において不良品の発生する確率はどのくらいなのかを数値であらわしたもので、数値が高くなるほど不良品がでる確率は低くなる。

自動車業界では一般的にCpkで1.33以上を要求される。
ちなみにこの時の不良発生確率は0.006％である。

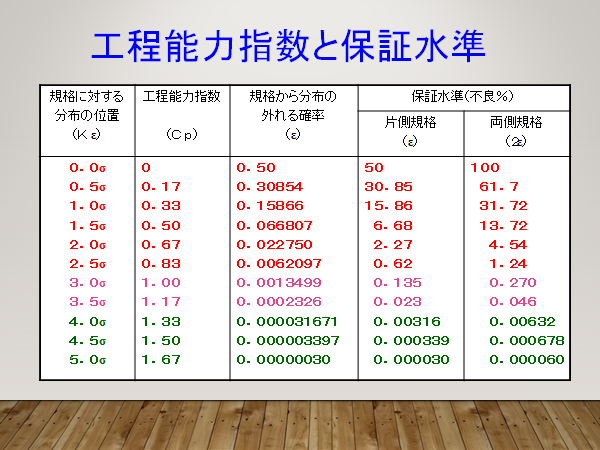
この確率が高いと感じるか低いと感じるかは人によって違ってくるであろうし、仮に工程能力が2あろうが10あろうが所詮は統計学の範疇であり、現場では突発的な不良、例えば金型や刃物の破損や切り粉の噛み込みによる寸法不良等、は必ず起こるし防ぎようがないのであるが、杓子定規な品質保証担当者は机上の工程能力確保厳守の一点張りで、本質に目を向けていないことが多くある。

そんな中で実務を行っていて厄介になるのが、工程能力と工程性能の使われ方が会社によっても担当者によっても違ってくる。
よくあるのは、既存工程では工程能力を、新規工程では工程性能（Ppk1.67以上）を評価せい、などど言っている会社が多い。
コアツールの教科書を読んでみると、単純な理解方法として、工程能力とはあるロット内の変動で、工程性能は異なるロット間も含めた変動と理解できる。
そうすると工程性能というのはかなり厄介である。製造目線からすれば、金型や刃物は摩耗を考慮してアッパーサイズに製作するのが理想であるし、研削加工では手直しなどを考慮して規格上目を狙うのが常である。熱処理に至ってはもはや条件でロット間のばらつきを制御するのは無理がある。
それはさておき、この二つの指標の実際の算出方法の違いはどのようになっているのであろうか？

計算式の違い
何と工程能力と工程性能は算出方法（計算式）は同じである。では何が違うのかというと、計算に使用する標準偏差の求め方が異なる

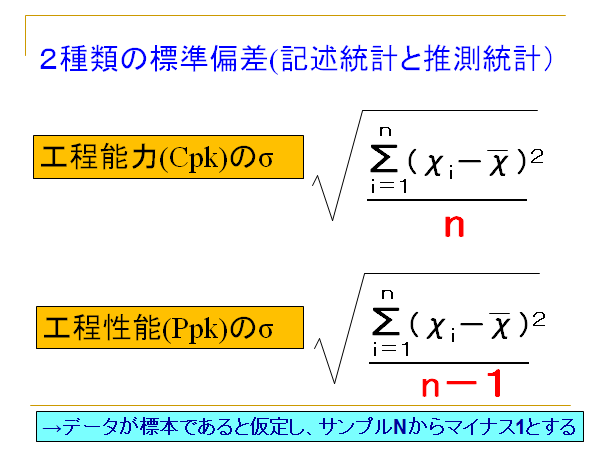
工程能力：母集団の標準偏差を使用→Ｎ数そのままで割る
工程性能：標本から母集団を推測して補正した標準偏差を使用→Ｎ-1にして割る

すると工程能力より工程性能の標準偏差のほうが大きくなる。よって大きい数値で割っている工程性能の方が低い値になる＝より厳しくなるというからくりである。
違いはサンプル数をNとするかＮ-1とするかだけである。

実務上はエクセル関数のフォーマットで算出している方がほとんどであろうが、その違いは標準偏差を求める関数の違いだけである。

例えば工程性能で評価する新規工程では、どんな変動要因があるかわからないから、保険をかけて工程能力数値を少し低めに算出しておこうといった解釈ができる。

では実際の数値にどの位の差がでるのかというと、一般的に良しとされているサンプル30本あればCpkとPpkの差は0.03程度の差、つまりほぼ差はないといえる。

これを理解していないと、Ppkは1.67以上必要である、などといったおかしな要求がまかり通ってしまう。
何が言いたいかというと、Ppk1.67以上を要求するということすなわちCpk1.67以上を要求しているのと同じことなのである。

しかしこの論理を逆手にとれば、Ppkは意図的に良い数値を選定して算出してもいいともとれる。
あくまで標本であるのだから、たまたまサンプルが良い数値に偏っていたというこじつけも可能であるのではないだろうか？
実際そんなことはしないであろうが、こういう考えをもっておけば少しは実務が気楽になるかもしれない。