今回は工程能力業務を効率的かつ効果的に行うための数値捻出方法についてご紹介しよう。
厄介な工程能力業務
製造業のお勤めの方で、特に品質保証部門のお仕事をされている方であれば、事あるごとに工程能力に携わっていることであろう。
新製品の立ち上げや既存ラインの定期的評価、不具合対策時の評価など多岐にわたっている。
評価項目にしても図面全特性ともなれば膨大な項目の測定データが必要となってくるので、とても一筋縄ではいかないわけであるが、そのコストもばかにならないのであるが、客先はそんなことはおかまいなしに平気で要求してくる。
実務を行う立場からすれば、さすがに律儀に全部を測定しているわけにはいかなくなってくる。
かといって全く測定しなければ現物とデータ資料に乖離がでてしまい、後で問題が発生した時に指摘されてやっかいなことになりかねない。
いかに現物と整合性のあるデータをつくれるかがカギとなる。
手法と考え方
この手法は、少数のサンプル実測値、概ね5個程度のサンプルからの実測値を利用して、その数値から適度にばらつきをもたせた数値を捻出していく方法である。
どの程度のばらつきをもたせるか、狙い値はどの程度にするかについては、要求されている工程能力数値と工程の特徴を加味する必要があり、これにはそれぞれの工法の知識や経験が重要になってくる。
それぞれの工法によっては、必ずしも正規分布になるとは限らない、むしろこの界隈においては綺麗な正規分布を描くことはまれであるのではないか。
重要なことはその工程のデータ分布がどのような傾向になっているかを常日頃から把握しておくことである。
こうすることで現物と明らかに異なる資料になってしまうことを避けながらも実務の負担を軽減させることが可能となる。
工程の特徴とサンプリング数値がきまれば、あとは数値を捻出していく作業になるわけであるが、これがまた厄介な作業になる。
適当に思いつきで入力していくと、意識しているつもりでも偏りが発生してしまうし、分布もおかしくなってしまう。
そこで、この問題を解決しつつ楽に作業できる方策として、エクセルの乱数関数とヒストグラムを使用した方法を例題を用いてご紹介しよう。
例題を基にした解説
例題
フライス加工部分の表面粗さの工程能力を算出する。
規格はRa6.3以下とする。
この工程からランダムにサンプリングした5個の数値は下記とする。
- 1.09
- 1.32
- 1.15
- 1.22
- 1.50
工程の傾向把握
まずこの工程の傾向を把握する。
フライス加工であるので、粗さの能力は加工条件と刃物の摩耗状態でほぼ決定する。
加工条件はほぼ固定されているはずであるから、新品の刃物と交換直前の刃物で加工した際のおおよその数値が把握できればよい。
今回は新品刃物の状態がRa1.00、命数到達時の状態がRa4.00としよう。
これをヒストグラムにすると、概ね右肩さがりのグラフになることがわかる。
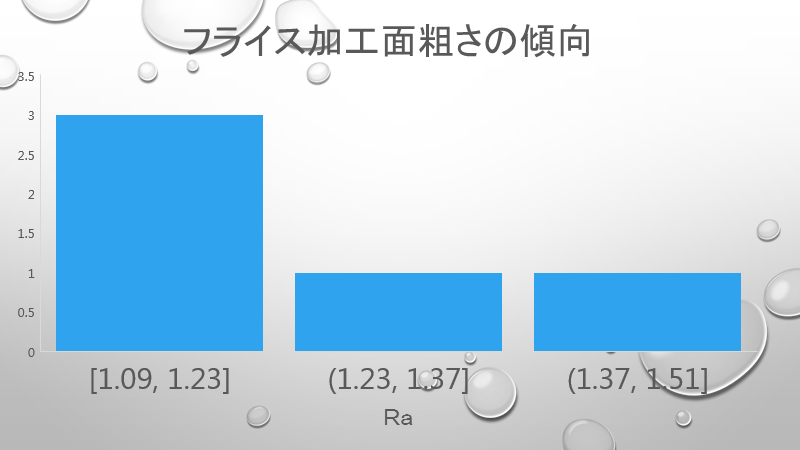
さらに切削刃物の摩耗というのは、常に一定の割合で進行するわけではなく、ある時点をさかいに急速に増加していく特性があることを考慮すると、粗さ数値の割合としては初期値の割合が多く、終盤につれて割合は小さくなるであろうことがわかる。
よって大まかに振り分けるとして、Ra1~2が7割、Ra2~3が2割、Ra3~4が1割として見積もろう。
エクセルシートへの入力
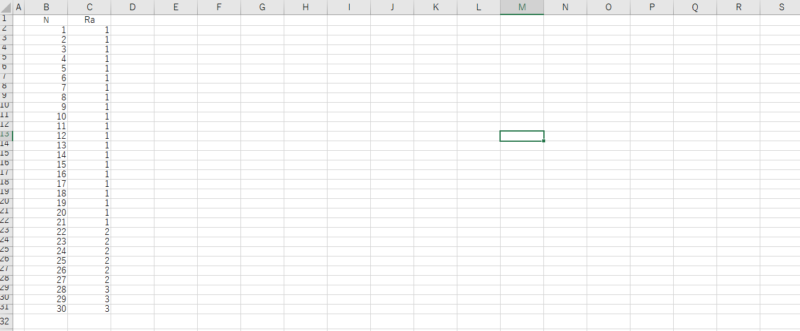
これをエクセルシートに下図のように入力する。
30個分の数値を算出するとして、7割にあたる21個に1、2割にあたる6個に2、1割に当る3個に3を割り当てる。
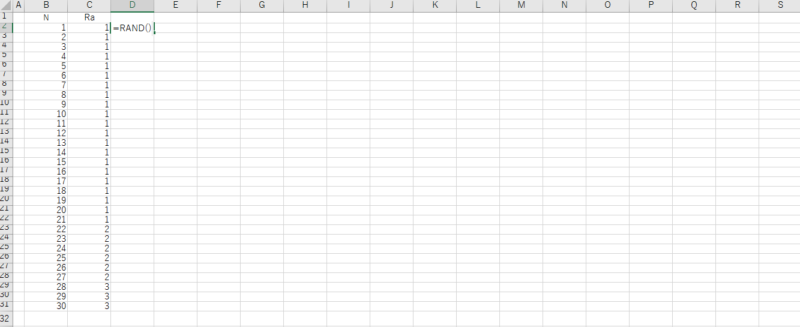
隣のセルに乱数を作成する関数、RAND()を入力する。これは小数点以下の乱数を発生させる関数である。
この2つを隣のセルに合計し、必要ない小数点以下を、ROUND()関数で切り捨てておく。
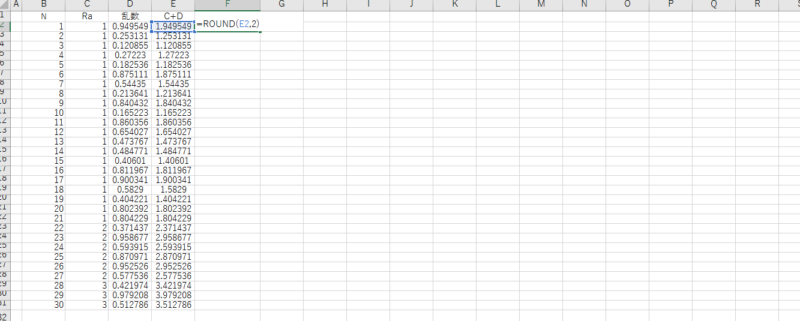
これによって工程能力数値の捻出ができたので、これをヒストグラムにして分布を確認する。
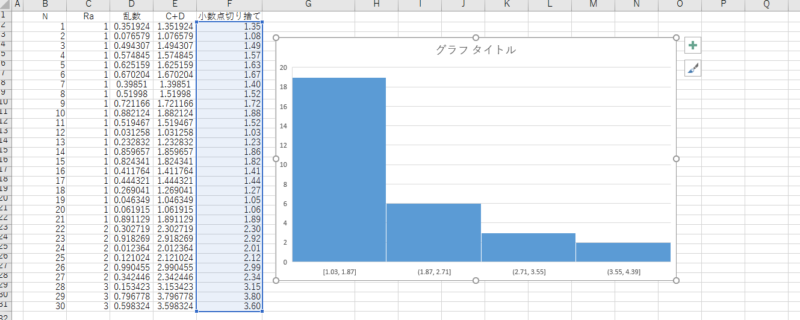
乱数は再計算(適当な空白セルをダブルクリックして戻るだけ)の度に変化するので、きにいった分布が出現するまで何度でも簡単に変更できる。
あとはこの数値をコピーして、各々の工程能力算出フォームのほうに値として貼り付ければ完成である。
品物によっては同種の測定ヵ所が何十カ所にも及ぶような場合もあるが、この手法を使えば効率的に業務を遂行することが可能になるであろう。
注意点
注意点としては測定値のエビデンスが必要ないことが前提となる。
まれに測定画面の波形や数値を印刷した資料を要求してくる厄介な輩も存在するので、その場合はおとなしく測定するしかないだろう。
それと例えばアナログダイアルゲージでの測定の際は、その読み取りの性質上、数値の端数は大抵0か5になるであろうから、その辺も予め考慮されたい。











